Gallery
Hopf Fibration (May 2009)
Here are some pictures of the Hopf fibration:


If you think of the Hopf fibration as a fibration of the Heisenberg group, it makes sense to look for characteristic curves on the Hopf tori. Here's what happens (notice they some times close up):
Here are some more characteristic curve demonstrations:



Lens Spaces (May 2009)
Rotate two copies of C^2 at different rates. Projectivize so you're now acting on CP^1. Take a quotient, and you have a lens space:

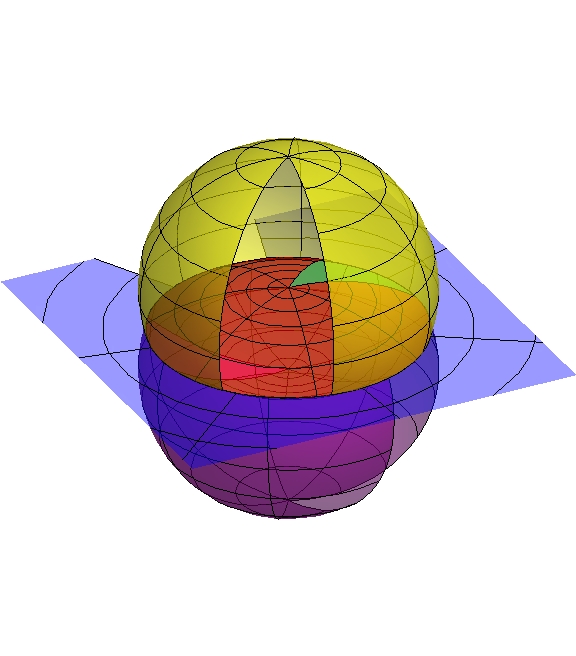
Here's what the rotations look like:
Heisenberg group (Summer 2009)
The Heisenberg group is R^3 with a strange structure: you're only allowed to travel along these planes (seen from different sides):


Spheres look like applies, and have cores (usually known as "bubble sets").


Recall that you draw a unit sphere centered at 0 by taking a segment of length 1 and finding its endpoint. As you drag the segment around, you trace out the sphere. The sharp points on the sphere are due to having lots of ways to get there. And the bubble set keeps track of these: it's exactly all the segments going up to the sharp point.
Generally, there are infinitely many ways to travel between two points. The only sets in the Heisenberg group that are convex are: the empty set, single points, and the whole space. Bubble sets aren't convex:

A standard trick is to give the Heisenberg group a Riemannian structure: to allow just a little bit of traveling away from the planes. Here are the calculations of geodesics that are behind the following animations.




