Gallery
Mathematical Models (2012-2013)
3D printing and laser cutting leads to fun toys:


The wooden cube consists of six Sierpinski carpets, made using a laser cutter at UCLA. It represents a Menger sponge, which you could make if you had a block of wood and a really good laser cutter (current ones can't cut too deep without burning the wood).
The other models are objects in Heisenberg geometry that Joseph Vandehey and I found while studying Heisenberg continued fractions. The "flower" shape is an inverted cube, and the other objects demonstrate tilings of 3D space by tiles with Heisenberg group symmetry. These were printed on the 3D printer belonging to the Illinois Geometry Lab.
Complex hyperbolic space and the Heisenberg group (Spring 2012)
A Lagrangian plane in complex hyperbolic space (used to build packs):
Boundaries of packs in the Heisenberg group:
For some explanation of the pack videos, see the You-tube descriptions or read Platis's 2008 paper.
Physics in hyperbolic 3-space (spring 2011)
Mathematica and POV-Ray, with the help of Platon Lukyanenko
In hyperbolic space, things look smaller as they get closer to the XY plane, so a ball traveling straight will look like it's changing size and moving along a curved line. Collisions are defined infinitesimally by Euclidean physics, but these have to be adjusted for non-infinitesimal objects. In the simulation, the balls can't bounce out of the green sphere. The video below shows the same balls from a different view, where hyperbolic space fits entirely within a single sphere.
Complex hyperbolic space (summer 2009)
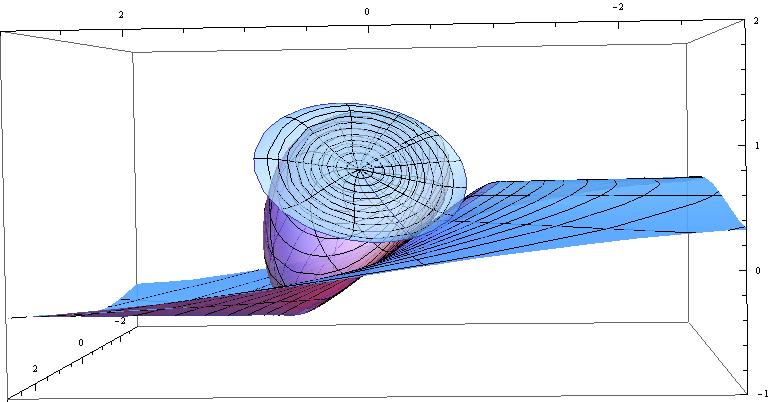
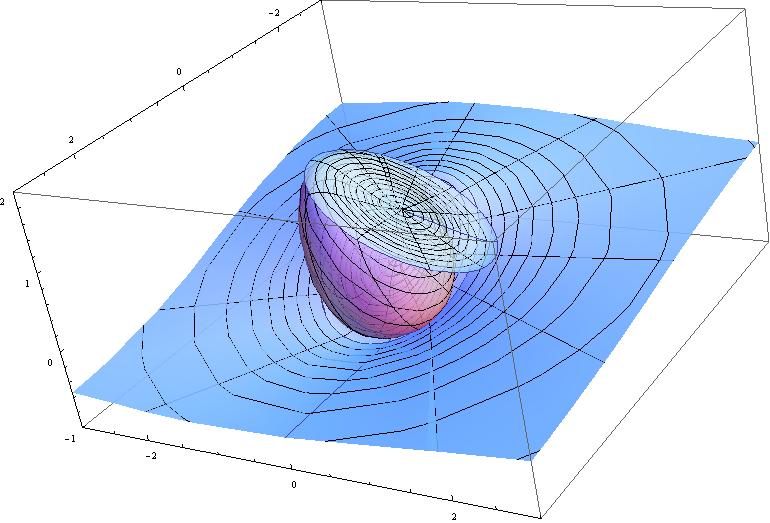
Complex hyperbolic space is 4-dimensional, so its geometric objects are often viewed on its boundary, the Heisenberg group. The Heisenberg group is 3-dimensional, but has a strange geometry. Here are some spheres in the gauge metric:
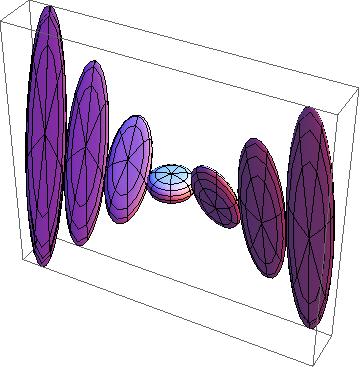
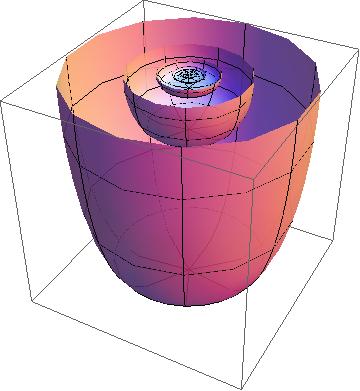

Metric spheres are examples of spinal spheres, which are boundaries of complex hyperbolic bisectors. The z-axis is the spine of the first sphere; the spine of the second sphere is shown:
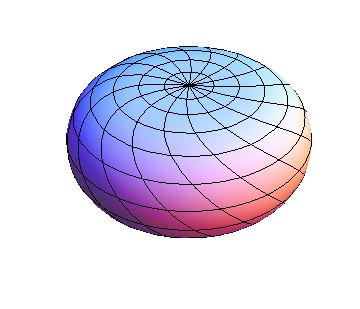
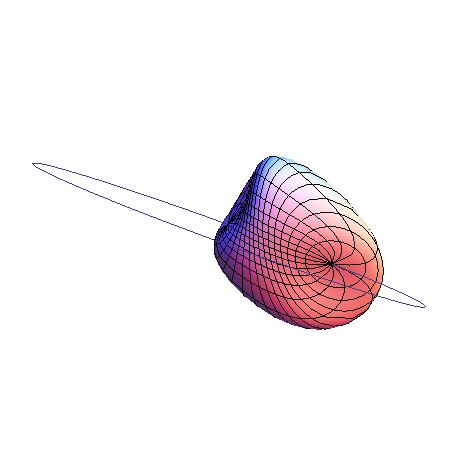
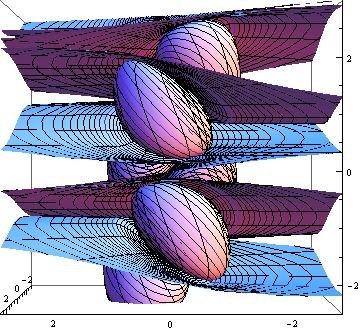
There are lots of objects I don't understand very well. For example, extors (which are a bit hard to draw):
The object at the end of the animation is a Clifford torus:
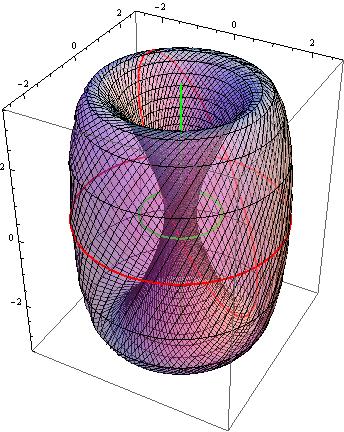
There are also C-spheres, foliated by C-circles (chains):
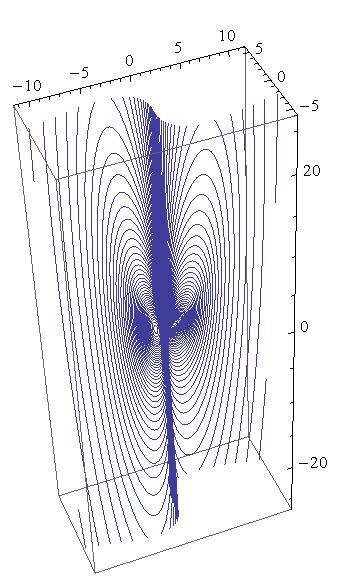
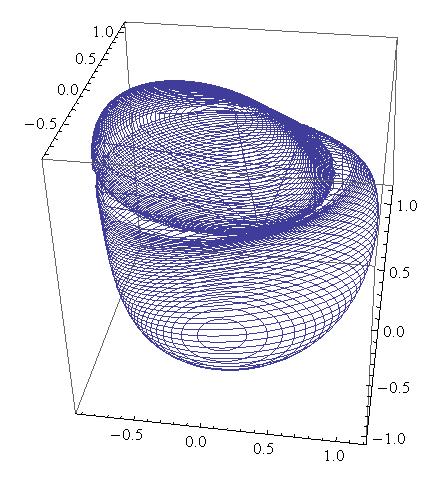
One can use the boundary to view fundamental regions for surface groups acting on complex hyperbolic space. The following pictures demonstrate an action on complex hyperbolic space of a 443-triangle group: